Equations for modeling DC phenomenona

Using the physics and appropriate mathematics to calculate a set of measurements is called “forward modeling.” The DC resistivity forward modeling problem involves describing potentials everywhere as a function of conductivity in the ground, geometry, and input current. It requires three fundamental relations:

\[\begin{split}&(a) \quad \textbf{J} = \sigma \textbf{E} \quad &&\textrm{Ohm's Law} \\[0.4em] &(b) \quad \textbf{E} = - \nabla V \quad &&\textrm{The electric field is the negative gradient of a scalar potential.} \\[0.4em] &(c) \quad \nabla \cdot\ \textbf{J} = - \partial{Q} / \partial{t} \quad &&\textrm{The divergence of current density equals the rate of change of free charge density.}\end{split}\]

We want to obtain a differential equation and boundary conditions to define the forward problem that will allow us to relate conductivity everywhere to potential everywhere. Start by combining (a) and (b) to say \(\textbf{J} = \sigma \nabla V\), then plug this into (c) to get

\[\nabla \cdot\ (\sigma \nabla V) = \partial{Q} / \partial{t} \quad (2)\]

This holds for steady state conditions everywhere, except at the source position \(r = r_s\), where it equals the input current, \(I\). In other words, charge does not accumulate under steady state conditions, except at the point of the source.

Equation (2) can be re-written as

\[\nabla \cdot\ (\sigma \nabla V) = I \delta (r-r_s) \quad (3)\]

The Dirac delta function is used here to indicate that charge density is varying only at the point source of current.

Boundary conditions that must hold are:

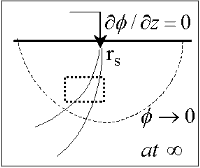
1. The change of potential across the free surface is zero (\(\partial{V}/\partial{n} = 0\) at \(z=0\)), and

2. \(V\) approaches 0 as \(r - r_s\) approaches infinity.

This differential equation (3) and the two boundary conditions define the forward problem that relates conductivity everywhere in the ground to potential measured anywhere within or on the surface of the ground. This problem can be solved numerically using finite element or finite volume techniques.

References

Dey , A. and H.F. Morrison, 1979a, Resistivity modelling for arbitrarily shaped two-dimensional structures, Geophysical Prospecting, 27, 106-136.

Dey, A. and H.F. Morrison, 1979b, Resistivity modeling for arbitrarily shaped three-dimensional structures, Geophysics, 44, no. 4, 753-780.

McGillevry, P.R., 1992, Forward modelling and inversion of DC resistivity and MMR data, unpublished PhD. thesis, UBC.