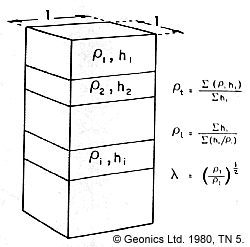
Anisotropic ground

Structural anisotropy (for example, layering or fracturing) causes the simple form of Ohm’s law to break down because current flow is not necessarily parallel to the forcing electric field. Instead of simply writing \(J = \sigma E = - \sigma \Delta V\), we have to write

\[J_i = -\sigma_{ik} \frac{\partial V}{\partial x_k} \quad i,k = 1,2,3\]

In homogeneous ground with a single current and potential electrodes, the expression for \(V\) (voltage) in terms of resistivity and distance from the current source is \(V=-I \rho / 2 \pi r\) (which was shown above). In anisotropic ground, there are different values of resistivity for the horizontal and a vertical directions. The expression for voltage in terms of the two resistivities and distance is

\[V=-I \frac{\sqrt{\rho_h \rho_v}}{2 \pi r} = - \frac{I \rho_h \lambda}{2 \pi r}\]

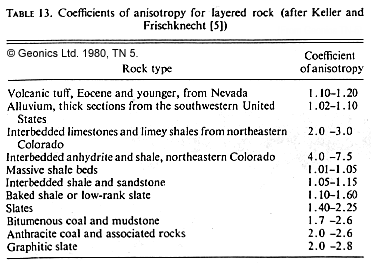
where \(\lambda = (\rho_i / \rho_h)^{1/2}\) is called the coefficient of anisotropy. See the table below for some values of \(\lambda\) encountered in common geological materials.