Electrical Conductivity
Electrical conductivity (\(\sigma\)) is a physical property that describes how easily electric currents can flow through a medium when subjected to an applied electric field. More specifically, it defines the relationship between the electrical current density (\(\vec J\)) within a material, and the electric field (\(\vec E\)) :
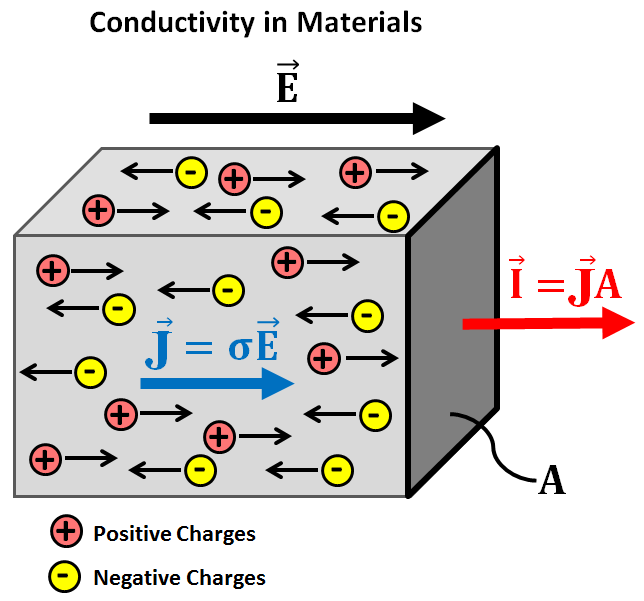
Within rocks and other materials, there are free electrical charges. When an electric field is applied to a material, these charges experience an electrical (Coulomb) force. This force causes the free charges to move through the material along the direction of the applied field; with positive charges moving parallel to the field and negative charges moving in the opposite direction. The size of the flow of electrical charges through a material is known as electrical current (\(\vec I\)). Current density represents the amount of current flowing per unit cross-sectional area (\(A\)), where:
In conductive materials (larger \(\sigma\)), free charges move quite easily and strong currents may be induced by a relatively weak electrical field. In contrast, resistive materials (smaller \(\sigma\)) require strong electrical fields in order to produce any significant current.
Resistivity: An equivalent physical property to the conductivity is the resistivity (\(\rho\)). By definition, the resistivity of a material is the reciprocal of its conductivity:
Both the electrical conductivity and resistivity are acceptable for describing the conductive properties of rocks and they are sometimes used interchangeably. Parameters used to define the conductive properties and their associated S.I. units are summarized below.
Property |
Symbol |
Units |
|---|---|---|
Electric Field |
\(\vec E\) |
V/m |
Current Density |
\(\vec J\) |
A/m \(\!^2\) |
Electric Current |
\(\vec I\) |
A |
Conductivity |
\(\sigma\) |
S/m or mS/m |
Resistivity |
\(\rho\) |
\(\Omega\cdot\!\) m |
where V is volts, A is Amperes and S is Siemens. Millisiemens per meter (mS/m) are often used (1000 mS/m = 1 S/m). Thus 1 mS/m = 1000 \(\Omega\cdot\!\) m.
Conductivity Measurements
Measuring a rock’s conductivity/resistivity is fairly straightforward. First, a cylindrical core sample is taken from the rock. The core sample is then placed in a sample holder between two copper/graphite electrodes where it acts as a resistive element for a circuit.
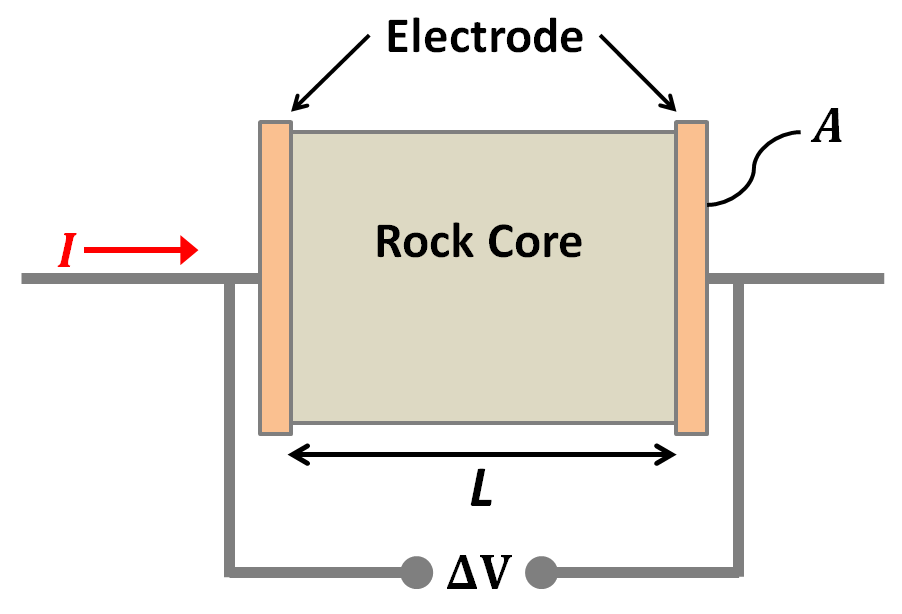
Next, a source is used to drive direct current (\(I\)) through the core sample. By measuring the voltage drop (\(\Delta V\)) accross the length of the sample, Ohm’s law can be used to determine the circuit resistance (\(R\)) caused by the rock:
The measured resistance increases proportional to the length (\(L\)) of the core sample. We expect this given that the current must flow through more of the resistive material. The measured resistance is also inversely proportional to the cross-sectional area (\(A\)) of the sample. This relationship can be understood by comparing the net resistance of two identical resistors in parallel to a single resistor in series.
Ultimately, the resistivity of the sample can be obtained from the measured resistance, the length of the core and its cross-sectional area using Pouillet’s law:
Conductivities of Common Rocks
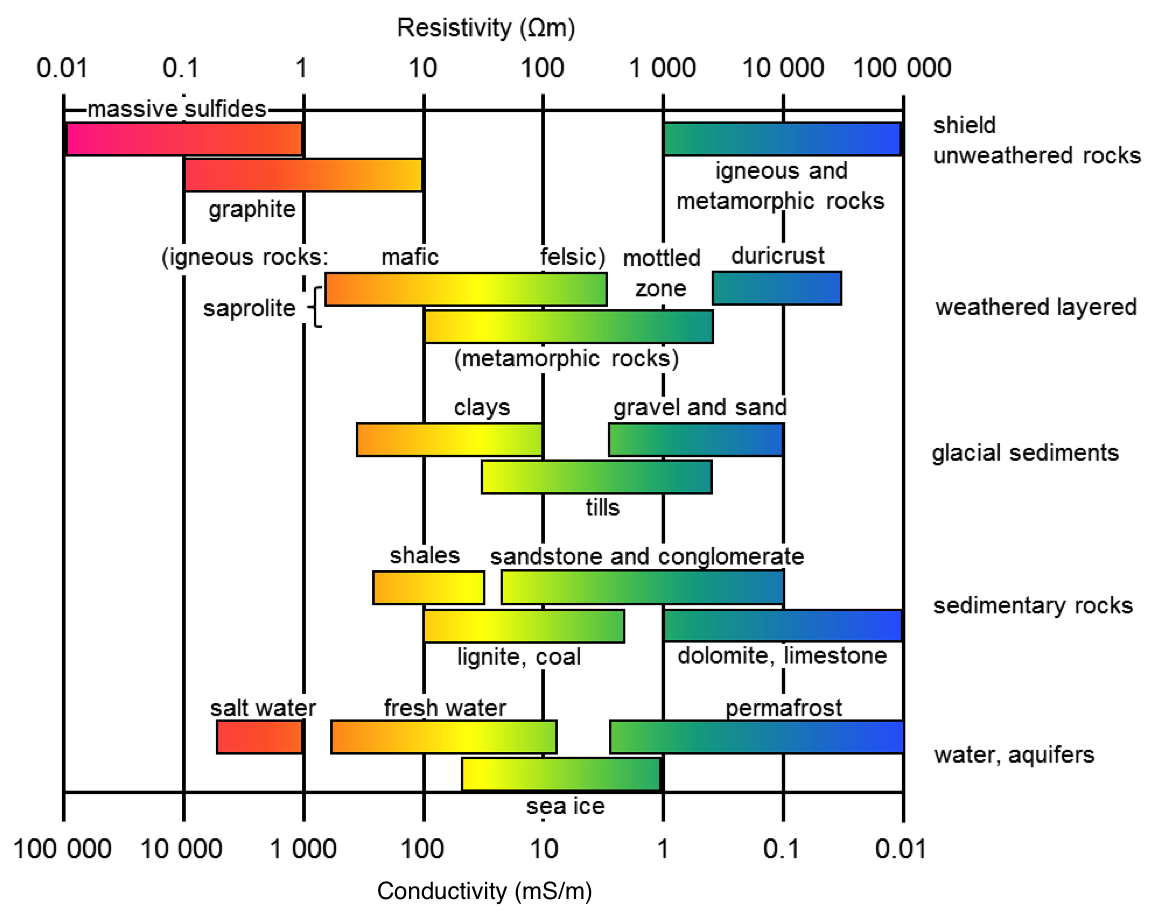
A chart showing the range of electrical conductivity/resistivity values for common rock types is shown below. Note that the scale is logarithmic, indicating a huge variability in conductivity/resistivity among rocks. From this chart we can infer several things:
Massive sulphides and graphite-bearing rocks are by far the most conductive.
Carbonate rocks and unconsolidated sediments are very resistive
Weathered igneous and metamorphic rocks are more conductive than unweathered igneous and metamorphic rocks.
Sedimentary rocks containing clays are generally more conductive.
Salt water is more conductive than fresh water.
Factors Affecting Rock Conductivity
Porosity, Pore Saturation and Pore Fluid
Most rocks contain pore-spaces which are at least partially saturated with ionic fluids. These fluids include: fresh water, brackish water, ocean water and brine. Because pore fluids have a higher conductivity than most rock-forming minerals, electrical current generally prefers to flow through the pore-space whenever possible. As a result, the bulk conductivity of the rock depends significantly upon its porosity, fluid saturation and the type of fluid contained within the pore-space.
For rocks which are unsaturated, the pore space is occupied solely by air. Because air is very resistive, it forces the current to flow through the minerals comprising the rock. As a result, unsaturated rocks are poorly conductive. When a sufficient percentage of the pore-space is saturated, the pore fluid is able to offer a more efficient pathway for the current. Thus, the bulk conductivity of rocks generally increases as fluid saturation increases.
Current flows through a rock’s pore-fluid via ionic conduction. As a result, the conductivity of the pore-fluid depends on the concentration of dissolved ions. Pore-fluid conductivity increases as the concentration of dissolved ions increases. This implies that rocks containing more brackish pore fluid are more conductive than rocks containing fresh-water.
Tortuosity
Tortuosity defines the connectivity and complexity of a rock’s pore-space network. For rocks with low tortuosities, the current’s path through the pore space is simple; resulting in efficient conduction of electrical charges. For rocks with high tortuosities, the path the current must take to get through the rock is very indirect. As a result, conduction is inefficient, and the rock is more resistive.
Mineralization
Electrical current within a rock will choose not to flow through the pore-space if the rock forming minerals are more conductive. This occurs frequently in ore-bearing rocks due to the presence of metal-oxides (magnetite, illmenite, specular hematite), metal-sulphides (pyrite, pyrrhotite, galena) and native metals (gold, silver, copper). One exception is graphite, which despite being entirely comprised of carbon, is very conductive. As expected, the conductivity increases as the concentration of conductive minerals within the rock increases.