Other aspects of gravity surveying
The reference spheroid
The earth’s shape can be approximated by an oblate (squashed) ellipsoid approximating mean sea-level. The “flattening” of the ellipsoid is at the poles; i.e. radius at equator > radius at poles. The reference spheroid is described by the following equation, which gives the theoretical value of gravity as a function of latitude \(\phi\). Coefficients were standardized in 1979, but earlier work may have used other coefficients. Plugging in 0 and 90 degrees yields approximately 9.780 m/s2 and 9.832 m/s2for values of gravitational acceleration at the equator and poles respectively.
The gravimetric geoid
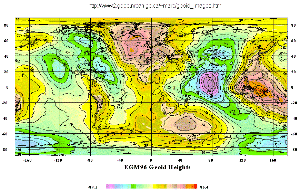
The surface of equal gravitational potential can be thought of as mean sea- level. It includes the influence of local density changes and trenches and mountains and is referred to as the geoid. Calculating the geoid is important for leveling and surveying jobs that require extreme accuracy. There is an entire division of Canada’s Department of Natural Resources called the Geodetic Survey Division. The link contains a huge amount of information on geodetic surveying, GPS surveying, and related material.
Marine gravity
On ships, gyrostabilized platforms are required since external accelerations (roll, pitch, and yaw of the vessel) can be as large as 100,000 mGal. Long- term averaging and damping suspension systems reduce vertical acceleration errors to 1 mGal. Cross-coupling error occurs for beam-supported mass instruments, since circular vertical motion induces torque that does not average out in the up-down cycle of floating over waves. The Bell marine gravimeter eliminates cross-coupling since it is axially symmetric. It can discriminate anomalies of 1-2 km wavelength, but it is expensive.
Airborne gravity
All problems caused by moving platforms are even more difficult to deal with for airborne work. Current best resolution is in the range of 0.1 mGal. The Eötvös effect can produce errors of 18 mGal or 25 mGal at speeds of 200 knots for 1% error in velocity or heading. Therefore, autopilots are required.
Since 1998, airborne instruments have become capable of acquiring data with sufficient resolution to contribute towards resource-scale projects. For example, there is a good deal of interest in using airborne gravity mapping to characterize salt domes for petroleum exploration applications. You could probably find examples on the web by searching for “gravity,” “airborne,” and “petroleum,” for example.
Gravity gradiometry measured from the air is a “last frontier” in gravity data acquisition instrumentation. In early 2000, BHP (one of the largest mining companies in the world, based in Australia) announced the development of the “world’s first airborne gravity gradiometer for mineral exploration.”
Satellite-derived gravity is also used in the exact characterization of the shape of Earth and other planets. See articles in the SEG’s January 1998 edition of “The Leading Edge” - for example, “Satellite-derived gravity: Where we are and what’s next.”
One field procedure that is not airborne gravity, but which uses aircraft to enhance the efficiency of acquisition (especially in rugged terrain) is helicopter-borne long-line systems. This involves an instrument hanging from a long wire which is placed on the ground for each measurement. Some of the advantages are: there are no cut lines needed; rugged terrain is easier to handle; the instrument is more gently handled than by a crew and truck; helicopter-borne GPS is just as accurate, and has more reliable signals in forested and rugged terrain. For finding the position of the instrument, a differential GPS unit finds the position of the helicopter, and ground reflecting laser altimeters compensate for the distance between the chopper and the instrument. Laser range-finding also has a better chance of getting accurate terrain at each station.
Gravity gradiometry
The gradients of Earth’s gravity field can be estimated from a simple map of gz by calculating horizontal first and second derivatives. Actually measuring the three gradients (\(g_z\), \(g_x\), \(g_y\)) may be desirable for several reasons.
However, interpretation of gravity gradiometry is not trivial. There was a whole session on this topic at the August 2000 annual meeting of the Society of Exploration Geophysics, and it is a current topic of research at several universities and oil & mineral exploration companies. One short paper on the topic is available from The Leading Edge (an SEG monthly publication) entitled “Methodology for interpreting 3-D marine gravity gradiometry data” in April 1999.
Other comments on instrumentation
Here are notes on characteristics of a modern, semi-automatic ground-based, portable instrument:
Many instruments now use a small solid state accelerometer, and the measure changes in capacitance due to varying spacing.
Sensors are in a controlled temperature vacuum; the quartz element temperature is monitored and corrected.
Instruments correct for leveling errors up to 200 sec of arc.
\(g\) is sampled at 1 s intervals and no result is displayed until it is deemed statistically reliable by the on-board micro-computer.
Movements are now “static,” meaning there is no need to “amplify” the mass movement, as is necessary with mechanical systems. Roughly 1% of mass support is by electrostatic feedback to keep it near the null position.
Automatic internal drift correction is commonly built-in, allowing for repeatability of 0.02 mgal over several months. Base station measurements are still needed to account for tidal effects.
Most systems now make use of digital storage of data, location parameters, drift, and computed tidal correction, all for download to a PC.
Absolute gravity measurements
Micro-g Solutions Inc. builds an absolute gravity meter that operates by using the free-fall method. An object is dropped inside a vacuum chamber and the descent of the freely-falling object is monitored very accurately using a laser interferometer. Specifications include:
Accuracy: 2 microGal (observed agreement between FG5 instruments)
Precision: 15 microGal/√(Hz) at a quiet site [e.g. About 1 microGal in 3.75 minutes or 0.1 microGal in 6.25 hours]
Operating dynamic range: world-wide