Gravity measurements

The physical property: density

Gravity surveys are usually done to find subsurface variations in density (kg/m³ or g/cm³). Densities of geologic materials vary from 880 kg/m³ (ice) (or 0 for air) to over 8000 kg/m³for some rare minerals. Rocks are generally between 1600 kg/m³(sediments) and 3500 kg/m³ (gabbro). Table 2.1 from PV Sharma is reproduced to the right.

It is important to recall the difference between mass, density and weight. Density is the physical property - it is mass (kilograms) per unit volume. Weight is the force experienced by that mass in the presence of a gravitational field. Your weight on the Moon is 1/6th of your weight on Earth, but your mass (and density) is the same wherever you are.

Fundamentals

We want to show that a mass above the earth experiences an attraction force due to Earth’s gravitational field. The phenomenon is described with very simple equations that were discovered empirically by Sir Isaac Newton in the 17^th century.

Newton’s equation describing the force between two masses (Earth and Moon, or Earth and you) is

\[F = G \frac{Mm}{r^2} \qquad \text{(Eq1)}\]

where the force \(F\) points from one mass to the other, \(M\) and \(m\) are two masses, and \(G=6.67*10^{-11}\) Nm²/Kg². You should recall that another of Newton’s relations characterizes the force on an object experiencing acceleration:

\[F=ma \qquad \text{(Eq2)}\]

Comparing these two equations, it should be clear that most of Eq1 represents an acceleration: \(a = GM/r^2\). In fact this is gravitational acceleration, and we call it \(g\). This gravitational acceleration \(g\) is nominally approximately 9.8 m/s² on Earth’s surface at the equator. Local variations in \(g\) will be caused by local variations in \(M\) and/or in \(r\).

Units

What are the units for this acceleration, or \(g\)? Acceleration is in m/s², but another name for g = 1 cm/s² is 1 Gal (short for Galileo). Usually geophysicists work in units of milliGals (0.001 Gal). You will also see the “gravity unit,” or gu, where 1 gu = 0.1 mGal. Some authors, especially in Europe, use gu’s instead of Gals. Earth’s gravitational acceleration in these units (converted from the more common m/s²) is 9.8 m/s²= 978 Gal, or 978,031.85 mGal, or 9,780,318.5 gu at the equator.

Measuring gravity

Measurable geophysical gravity anomalies generally range between 0.1 and 0.00001 Gal. This means we must measure accelerations of 1 part in 10 ⁸ or 10 ⁹; not a trivial task! How is this done?

If a mass hangs on a spring, a force on the mass \((F = ma)\) will stretch the spring. Hooke’s law states that the extension of a spring is proportional to force, or

\[m(dg)=k(ds)\]

where \(k\) is the “elastic spring constant,” \(dg\) :math:`` a small change in gravitational acceleration, and \(ds\) is a small change in spring length. So, if we measure \(ds\), we can get

\[dg = ds \frac{k}{m}\]

To summarize:

• The measured parameter is the force on a mass, \(m\), due to the presence of another mass, \(M\).

• The recorded parameter is acceleration, with units of milliGals (compared to m/s²).

• The interpreted parameter is usually density of causative buried materials and structures.

To carry out a gravity survey, you must measure this change in spring length all over the field site (or along a line). Then you can produce a map (or profile) of relative differences in gravitational acceleration, \(g\). Finally, this result must be interpreted in terms of variations in buried mass (integrated all over the volume), and/or in terms of the distance, \(r\), to the buried mass.

There are other fundamental measurements that do not involve springs. There are instruments that measure the time it takes for a mass to fall through a vacuum, and the period of a pendulum can be observed carefully. There are more details about these less common methods of measuring gravity in most text books about applied geophysics.

What is actually measured?

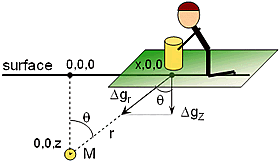
Instruments actually measure the vertical component of the gravitational effect of the target, \(\Delta g_z\). However, the formula \(Gm/r^2\) gives acceleration experienced in line with two masses, where r is the distance between center of masses (sensor and target mass). Since we measure \(\Delta g_z\) along the surface over the target, we must resolve this geometry. Using the figure to the right, \(\Delta g_z\) at location \((x,0 ,0)\) is

\[\Delta g_z = \Delta g_r \cos(\theta) = \Delta g_r \frac{z}{r}\]

and since

\[\Delta g_r = G \frac{M}{r^2}\]

then

\[\Delta g_z = G \frac{M}{r^3} = G \frac{Mz}{(x^2+z^2)^{3/2}}\]

If the mass, \(M\), is a sphere centered at \((0,0,x)\), then this equation describes the pattern of gravitational acceleration that would be measured along a traverse that crosses over the sphere. For a sphere with radius, \(R\), the mass and its density are related according to \(4/3(\pi R^3)dρ\) where \(dρ\) is density contrast; that is, density of host rocks minus the density of anomalous mass.

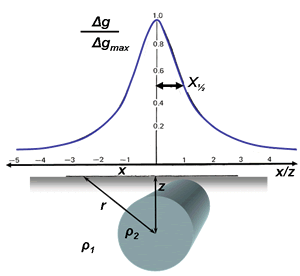
This relation (profile) is plotted (figure to the right) assuming the survey crosses over a 2D “point” mass - i.e. a “line mass,” or horizontal cylinder. The pattern would be similar but slightly narrower if the buried feature was a point mass or sphere.

• Note that the “mass” must involve the density contrast. In other words, the difference between host and target densities.

• An estimate of vertical depth to the center of mass can be obtained by equating amplitude at \(x=0\) to twice the amplitude at \(x\).

• The result is a half-width rule giving depth to center of a sphere \(z=1.3 x_{1/2}\), where \(x_{1/2}\) is half the width of the measured gravity anomaly at half of its maximum amplitude. You can prove this by recognizing that at the maximum amplitude (directly over the sphere), \(x=0\) so \(g_Z=GM/z^2\). Then \(x\) in terms of \(z\) at the location where \(g_Z\) is half of its maximum amplitude, or

\[\frac{GM}{2z^2}=\frac{GMz}{(x^2 + z^2)^{3/2}}\]

• For the infinite horizontal cylinder, the half-width rule is \(z=1.0 x_{1/2}\), giving depth to the center of the cylinder.

Factors affecting gravity

Gravitational acceleration measured at any point depends on five factors, all related to either \(M\) or \(r\) or both (in Eq2 above). The effects are as follows, and corrections for these effects must be applied to data sets. The section on data reduction explains further.

1. Latitude: From equator to pole, gravity varies by roughly 5000 mGal (greater at poles). The gradient (i.e. rate of change with respect to latitude) is maximum at 45° latitude, where it is about 0.8 mGal/km.

2. Elevation: The effect of changing the elevation (changing the \(r\) of Eq2) of a measurement is quite significant. For modern instruments, a change of only a few centimeters can be detected, and between sea level and the top of Mt. Everest, the difference is roughly 2000 mGal.

3. Slab effect: Going up in elevation rarely means up into air (except for airborne surveys). If we are “up,” there are rocks and soils between us and where we were. The attraction of these materials counteracts the effect of going up in elevation. Therefore, the elevation correction is counteracted by subtracting a factor of \(0.0419 \times h \times d\) mGal, where h is elevation in metres, \(d\) is density of intervening materials in g/cc. This is called the Bouguer correction.

4. Topography: Effects due to nearby topographic relief (hills or valleys) may be significant, but are rarely more than 1.0 mGal. These effects are rather tedious to apply, but are important when there is steep topography near the measurement locations.

5. Earth tides: Tidal effects are as much as 0.3 mGal, and these are usually accounted for by recording several measurements at a single station (a base station) throughout the course of a survey.

6. Lateral density variations: Large scale structural anomalies (basin and range geology) may be 100 - 500 mGal. Good targets for oil exploration (a salt dome) may be ~ 10 mGal. In mineral exploration, ore bodies may cause anomalies of around 1 mGal. A geotechnical application may involve anomalies of 20 microGal.

7. Effects of a moving platform: If the instrument is in motion while a measurement is made, the acceleration caused by motion on a rotating sphere must be accounted for. These contributions to measured acceleration can be very large, especially in aircraft. Even the slight rotational motion of a ship resting on a sea with mild swells will have significant effects on measurements.

As noted above, all data sets must be corrected for these effects, and this is discussed in a later section.