Migration

Migration

The ideal goal of seismic processing is to have a section which consists of true reflections which arise from structure directly beneath the source. The image should provide quantitative information about geologic structure. The vertical axis ideally is depth but generally the time-to-depth conversion is not carried out and the axis remains time. A processing step which is important in putting reflectors in their correct location is migration. The need for migration is most evident when layers are not flat lying. Consider a single dipping layer and seismic traces corresponding to a coincident source and receiver.

The reflection time is given by \(2l/v_i\). But when we plot the section we think of the reflections arriving from directly beneath the shot. The result is that a sloping reflector in the ground will appear as a sloping reflector in the seismic section, but the slopes will be different. The true dip will be greater than that observed on the section. The relationship between the two dips is

\[sin(\alpha_t) = tan(\alpha_s)\]

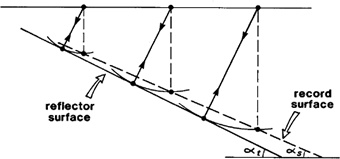
Fig. 82 A planar-dipping reflector surface and its associated record surface derived from a non-migrated seismic section.

Other artifacts are visible in non-migrated sections. Synclines will be observed as “bow ties.” Their width on the seismic section is narrower than reality and their structural depth is diminished. Conversely, anticlines will appear wider than they really are. Finally a point scatterer will be observed as a hyperbola.

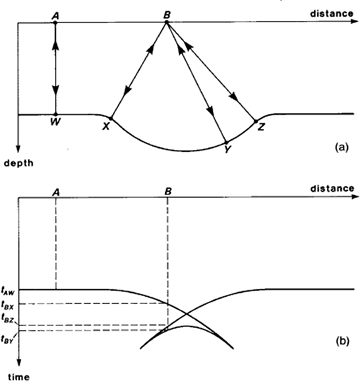
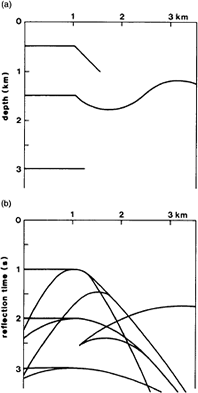
The plots above show several synthetic geologic structures and their associated non-migrated seismic sections: (a) a sharp synclinal feature in a reflecting interface, and (b) the resultant “bow-tie” shape of the reflection event in the non-migrated seismic section.

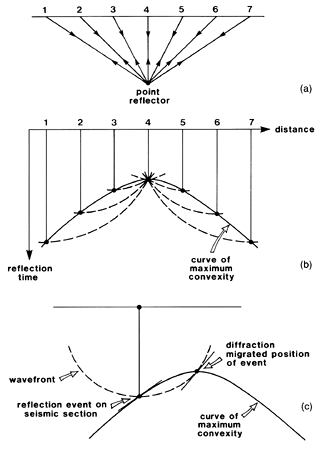
Migration is the process of reconstructing a seismic section so that reflection events are repositioned under their correct surface location and at a correct vertical reflection travel time. The effects of migration are to:

• collapse a diffraction hyperbola back to a point;

• make dipping structures appear with correct dip angle;

• remove the bow ties from synclines and

• shorten anticlines.

The principles of migration are shown in the figure below left. A single point diffractor will generate a hyperbolic trajectory in a travel time section. Migration collapses the hyperbolic event back to its apex.

The example above right shows an unmigrated section (top). The section after migration is shown in the bottom panel. 1

1

From Kearey, Philip and Micheal Brooks, “An Introduction to Geophysical Exploration.”” 2nd ed. Blackwell Science: 1991.