Basic principles

Effects of IP on Geophysical Measurements

To demonstrate the effects of induced polarization on geophysical measurements, consider a specific example where a current generator, hooked to the ground as in a DC survey, is turned on. At some location, the electric potential (\(V\)) is measured. In non-chargeable rocks, an instantaneous increase in the measured potential occurs when the source is switched on. When the source is switched off, the current through the Earth returns immediately to zero and so is the measured potential. This is illustrated in the figure below.

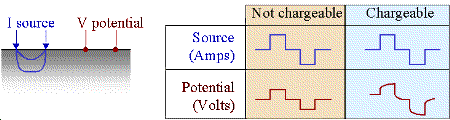
If the ground is chargeable, there will also be an instantaneous jump in the measured potential when the source is switched on; we denote as \(V_\sigma\). However, the subsequent build-up of ionic charges during the on-time results in a corresponding increase in the measured potential; which is sometimes referred to as the over-voltage. Eventually, the build-up of ionic charges reaches saturation, resulting in a final measured potential (\(V_m\)). In general, the measured potential after the source is switched (\(V_{on}\)) can be expressed as:

\[V_{on}(t) = V_\sigma + V_s \Big[ 1 - e^{-t/\tau } \Big]\]

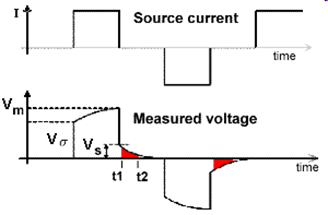
where \(V_s\) is the amplitude of the over-voltage and \(\tau\) is a constant which determines the rate at which the induced polarization forms.

When the source is switched off, there is an instantaneous drop in the measured potential equal to \(V_\sigma\). Subsequently, the accumulated charges begin to diffuse, resulting in a measured potential which decays according to:

\[V_{off}(t) = V_s \, e^{-t/\tau}\]

This decaying off-time potential is commonly called the discharge curve. We use the discharge curve to characterize the chargeable properties of the Earth.

Definitions for Chargeability

It is convenient to consider “chargeabilty” as an independent physical property but in reality it is an integral component of the electrical conductivity. It describes how the conductivity changes with frequency. If \(\sigma_0\) denotes the conductivity at zero frequency and if \(\sigma_\infty\) is the conductivity at infinite frequency then the chargeability is

\[\eta = \frac{\sigma_\infty -\sigma_0}{\sigma_\infty}\]

This is a dimensionless number varying between 0 < \(\eta\) < 1. It is often referred to as the intrinsic chargeability. The above definition is equivalent to defining the intrinsic chargeability as the ratio between the amplitude of the over-voltage (\(V_s\)) and the DC voltage (\(V_m\)):

\[\eta = \frac{V_s}{V_m}\]

The intrinsic chargeability for materials is rarely provided in tables. Rather, numbers based upon laboratory measurements of some characteristic of the induced polarization response is provided. Those measurements can be in time or frequency and the units of the “chargeability” are inherited from the data. We outline below: