Vertical Resolution
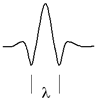
The vertical resolution of a seismic data sets describes how thin a layer can be before the reflections from its top and its bottom become indistinguishable. This depends upon the shape of the seismic source wavelet. The shape, or more particularly the signal wavelength depends upon the frequency and the velocity of the materials. Recall that \(\lambda = vt\).

Fig. 83 or
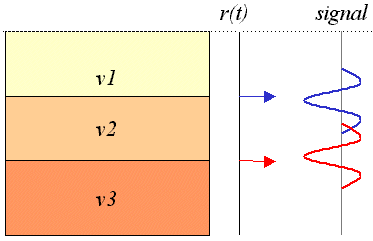
Vertical resolution is defined in a visual sense: that is, “can the two arrivals echoing off the top of the layer and the bottom of the layer be distinguished”? In the case to the right there will be no trouble seeing both returning wavelets because the time signals spent in layer 2 is such that the two pulses are far enough apart to be distinguished.
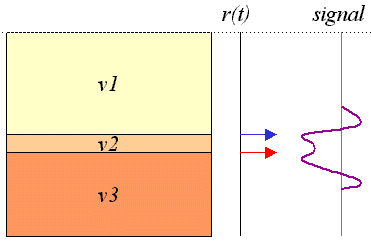
In the second case the two pulses overlap so the interpretation is of one layer only. Recall that we are depicting ideal situations with these figures. What is a minimum thickness for layer 2 before the two pulses overlap? Intuitively the two pulses will overlap unless the distance within the layer is more than a wavelength. Since the second pulse travels both directions this means that when layer 2 is 1/2 wavelength thick, the two pulses will arrive well separated.
In fact, the theoretical minimum thickness is 1/4 wavelength. In other words, careful processing can extract the pulses if they overlap by half a wavelength, but this theoretical minimum is never really achieved in practice.
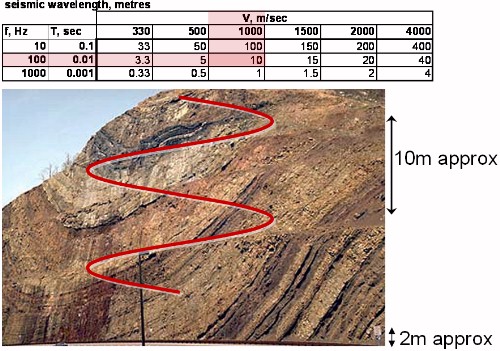
How does this thickness in terms of wavelength translate into real distances? As noted above, wavelength depends upon frequency of the signal and on velocity of the medium. Therefore the vertical resolution of a survey depends upon both the signals used and the materials themselves. The following image with its table of velocities and frequencies illustrates.